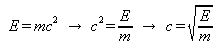Welcome to the wonderful world of fourth dimensional geometry. Purpose of this page is to have the reader acquainted with outline of four-dimensional time-space. This is done with different kinds of examples and playing with ideas. Farther on there will be dealing with connections between four-dimensional geometry and other sciences, such as physics, algebra and probability calculus. Meaning of these subjects is to give basis for examination of gravitation. But in the beginning there will be an introduction for history of the higher dimensions in science. History of Fourth Dimension and Scientific Emerging Fourth dimension has been known as a scientific concept as early as end of the nineteenth century, when had been started to examine physical and mathematical dilemmas with geometry of curved surfaces. Before this there had been only the Euclid geometry of flat surfaces. New concepts of non-euclid geometry were adapted into the comprehension about the physical world. World was not anymore thought as a space going directly forwards and where the object which does not change its direction never crosses its own path of movement. Study of geometry for spherical and convex surfaces was arising structures of ideas which could not be described in traditional three dimensions. There came a vision about existance of higher dimensions on beside of the three dimensions. The fourth dimension had been become a trend of the laity in the shift of nineteenth and twentieth century. This was especially emphasised among the idealism of spiritism. Effects of spiritualism did not only affect to the laity, but it had also its effect to scientists of that time. One of that times mathematicans, Charles Hinton, had took for his mission to develop visual aids that describes the fourth dimension. According to his words it would be possible to understand the four-dimensional time-space by meditating on them. As a mathematican he had understood that it is not possible to present a whole four-dimensional object in three dimensions, he intended to produce his pieces as shadows or squareroots of four-dimensional objects. Most famous of piece of his design is called as a tesseract. Shape of a tesseract is defined from a cube that is levelled off into a two-dimensional form. A cube is leveled off in a way that its faces collapse like a cardboard box and forms a cross. Two dimensional form will be raised to power. Final piece could be visualised in three dimensions because of the leveling off. 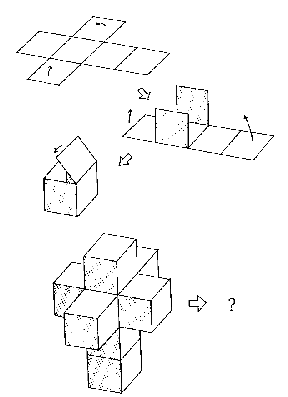Image from the book Hyperspace, written by Michio Kaku The meaning of tesseract was mixed in mysticism and symbolism. Despite of that it still is an operative mathematical model to some degree. Later on a tesseract and its structure will be dealt with to a larger extent. Other scientifically more important discovery of that time put forth an intellectual revolution. Einstein's theories of relativity overthrew ideas about absolute nature of time and space. With theories of relativity it was possible to describe gravitation as a curvature of geometric plane. The theories predicted curvature of light rays in a strong gravitational field. Curvature in path of ray of light was possible to explain with curvature of time-space continuum in a higher dimension. Image from the book Hyperspace, written by Michio Kaku Theories of relativity also changed the concept of time. Time is no more seen as absolute quantity that goes by with even speed, like sand in the hour glass. Gravitation affects also to passing of time. Generally fourth dimension is related to time in the theories of relativity. Time can be described as one directional coordinate where movement happens from the present to the future. Mathematical Logic of Dimensions Starting-point for finding a logical system is to look for a continuous structure. Mathematical structure is like a manual that tells how to visualize higher dimensional objects. If the logic is followed through three known space dimensions, then it is easier to find conception about fourth dimension's structure. Pascal's triangle gives clear reference to that what kind of structure each dimension's even sided forms have. 1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 If a piece with even sides has sides which length equals to sum of A and B, it is possible to describe dimensional structure by using algebra. Sum of values A and B raised to power of zero equals value of one. Highest number one in the Pascal's triangle describes the coefficient of power of zero. Sum of values A and B raised to power of one equals to multiplying sum with value of one. This means that raising to the power of one does not change the value. coefficients for values A and B are one and one, which can be found from the second line of the triangle. Sum of the values A and B can be visualized as segment of a line. Sum of values A and B raised to the power of two can be presented in a following form: "a^2 + 2ab + b^2". Coefficient of the a^1 is one, coefficient of ab is two and b^2 has coefficient of one. These coefficients can be found on the third line. Following equation can be visualized as a segmented square. 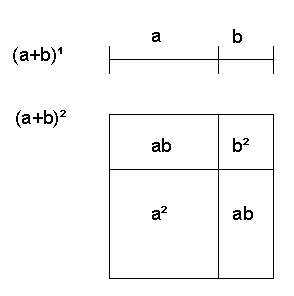Three dimensional piece has a structure that equals following equation: (a^3 + 3a^2b + 3ab^2 + b^3). This structure can be This structure can be taken to pieces, where dimensions of these pieces are as follows: a*a*a (1 piece), a*a*b (3 pieces), a*b*b (3 pieces), b*b*b (1 piece). Coefficients of these pieces can be found from the fourth line. 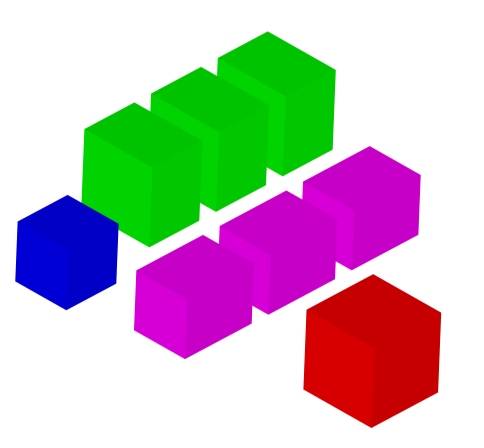It is always possible to create a cube from those pieces, regardless of the values A and B. Lower part of the cube equals to (a+b)^2 times the greater value. 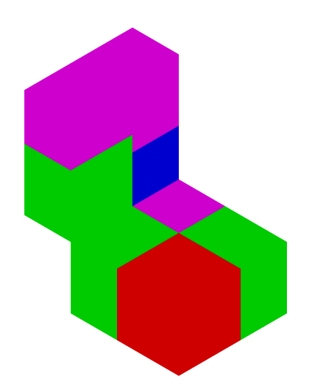From Cubes to Hypercubes Hinton's tesseract left uncomplete in that matter, there cannot be seen a model that is required by the logical structure. Symmetry of square and cube is evident, therefore a real hypercube can be predicted to be symmetrical. Structure of equation of fourth degree is on the fifth line of the Pascal's triangle: "1-4-6-4-1". There is no need for two values for finding the structure of hypercube. Value B that has been helping to visualize structures of lower dimensional structures, is no more needed. Equation of four dimensional piece will become more simplified, that is a^4. Important values for hypercube's structure are only "1 4 6 4 1" and a^4. 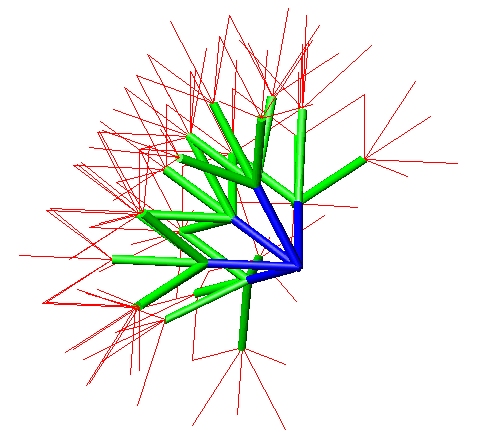To create a hypercube, it is a must to begin with a cross shaped piece, a cube that is leveled off to second dimension. This is the same structure from where a tesseract is compiled of. When combining cross-shaped pieces together, it is obvious that they do not create such a solid form like a tesseract. Closest shape to a tesseract is a structure which reminds of a tunnel with wings on the side. It requires six of these pieces to be placed from six orthogonal directions to compile a symmetrical structure. Hollow tesseracts produce overlapping layers when compiled. Before hollow tesseracts are combined, it is important to become aware of large amount of layers. Pieces are combined together in a way that wings are overlapping with the pieces that comes from below, above and the sides. Due to this only the outermost parts are not overlapping with any other pieces. 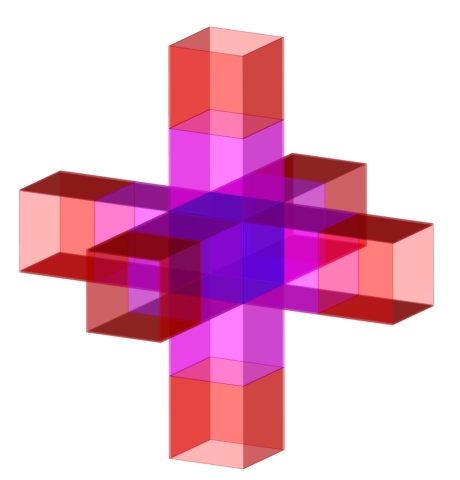Combining hollow tesseracts produces a hypercube. Hypercube is like an elevator shaft where elevator has six possible directions of movement. These directions represent movement possibilities of the cube within two perioids of time. Solid cube in the middle of the structure represents certain starting position. Areas next to that are primary possibilities where cube can move to. Outermost areas are secondary possibilities which require that movement to the primary possibility next to them has first occured. The cube in the middle has four layers for each of its faces. If each layer is counted as its own face, there is six times four layers, which makes total amount of twenty two layers. Each of primary possibilities have also four layers, but they have only four faces. Four times four makes sixteen faces. Secondary possibilities have only four faces, since there is no overlapping layers. Because hypercube in the example is a shadow of a four dimensional object, it also means that coefficient of four equals to rising to power of four in real four dimensional object. If all the faces are divided with four, then cube in the middle has value of six, primary possibilities have values of four, and secondary possibilities have values of one. Here is shown the structure which is from the Pascal's triangle: "1-4-6-4-1" 1 1 4 4 1 4 6 4 1 4 4 1 1 From Hypercubes to Hyperspheres Gradual steps of a hypercube do not exist as they are in the physical world. There objects move without steps. There are infinite variations of different directions and objects can revolve around their axis. Two spherical forms are shaped when object moves around its axis through all possible positions. Inner sphere describes the area which is always filled by the cube, despite of the rotation values. Outer sphere represents area what might partly be filled with the cube, depending on to what directions the corners are pointing at. 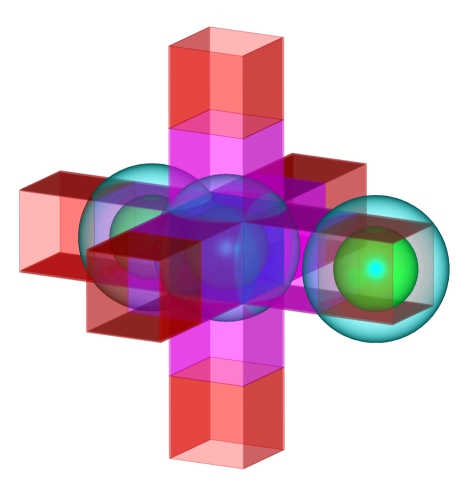When there are no any rules of movement applied, all objects have a spherical form in fourth dimension. Sphere is the most symmetric of all the shapes. Spherical form is shaped when all possible movement routes of future are drawn at the same time. 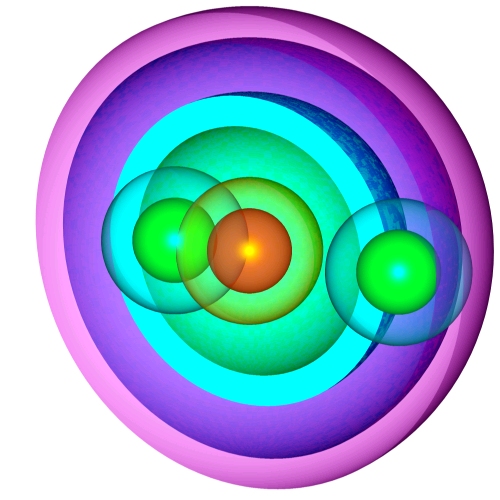Energy of an object will exist forever, so it could be said that an object can move forever, and so it has an infinitely large shape in fourth dimension. However, it is possible to determine a finite sample of a hypersphere, since object can move only as fast as speed of light. Radius of a hypersphere sample can be determined by multiplying the speed of light with the length of time. If sample of a hypersphere is taken within one second, it means that the size of a hypersphere sample is approximately three hundred thousand kilometers plus the length from the center of the object to the furthest part. 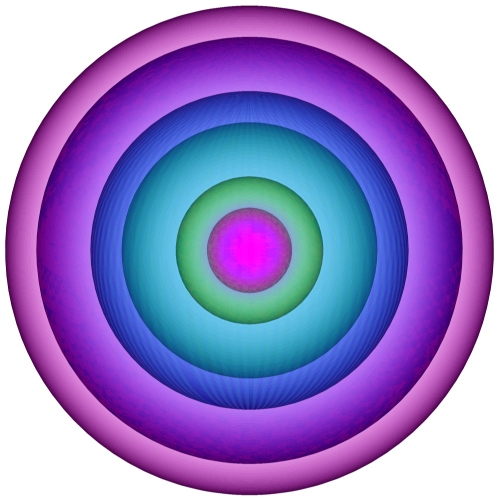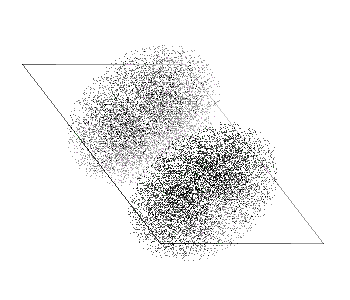Hypersphere consists of a center point core and a vast mantle. Mantle of the hypersphere is very sparse, where the core has very high density. Density inside a hypersphere is an indicator of a probability for object to move to that area. High density of the core indicates that it is practically certain for a hypersphere to maintain its central position. This is the general set for any hypersphere that does not interact with other hyperspheres. 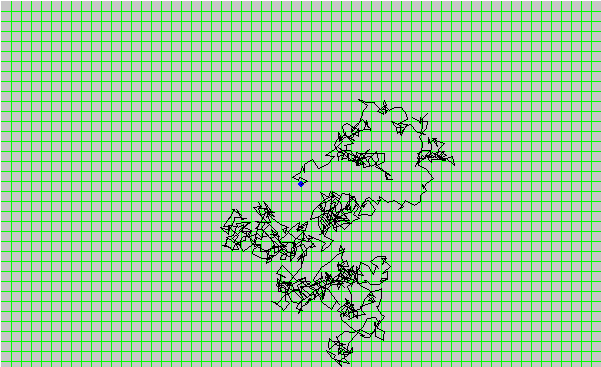Screencapture from Random Walk Generator There is movement in the center of a hypersphere, even if it cannot be noticed as a change of position. Generally movement is understood as a change of positions between two or many objects. This is called as relational movement. It is possible to define an absolute movement for an object, which is not dependent on comparison between other objects. Basic feature of the absolute movement is its haphazard directions. Haphazard movement does not have actual direction of movement, but it concentrates around the starting point. This can be proved with probability calculus. When there is taken a small sample of random behaviour, the average of these random values can vary a lot from the average of probability calculus value. The average of samples is approaching the average of probability calculus when more samples are collected. I this case the average of probability calculus is zero movement from original position. It is easier to understand result of the probability calculus by using model of two possible directions. 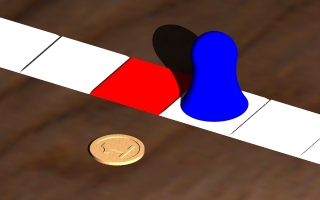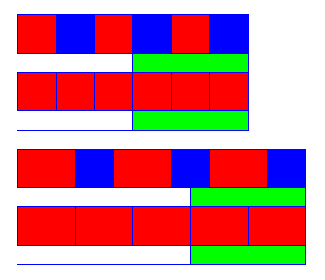Tossing a coin is an easy way to randomize movement into two directions. Two directions can be represented with a row of squares. When a coin shows heads, a piece is moved one square forwards, and when coin shows tails it is moved backwards. One throw with a coin showing tails nullifys one coin with heads and vice versa. The coin can be tossed many times and then count all heads and tails at once. If it occurs that there is as many tails as there is heads, then piece doesn't move anywhere from the starting square. Piece never moves far from the starting point since both directions are equally probable. In this example absolute movement is total amount of times when piece is moved to either direction. Relative movement is movement towards a specific direction. Absolute movement reminds of the concept of temperature, where atoms of a solid mass are moving without changing their position in the structure. The steps of movement are described with the squares of a game board. Relative movement is movement to a specific direction. Screencapture from Random Walk Generator Average dispersion of movement outwards from the starting point is depending on the length of a step. Dispersion that is change of position away from the starting point is very slight with short steps. When length of a step is infinitely small, which practically equals to zero, then there is no movement away from the starting point. This is true even if the speed of random movement is speed of light. Problems with describing the hyperspheres are the multitude of possibilities and lack of separate details. Perfect symmetry is like white paper or equally solid space. At the same time it describes everything possible but nothing specific. Therefore observation of absolute movement requires restrictions, such as orthogonal direction and steps of movement in hypercube model. One closed environment with move rules is chess. There are multitude of possibilities to make a move (as can be seen from the "Thinking Machine"). Computer uses cheer computing power and library of moves, but human brain makes the solution with a more intuitive way. Weather forecasts are one field of science that use lots of computing for the results. Here for example is an estimated area of a hurricane's path from (http://www.mapwatch.com/gallery/). Advantage brought by the restrictions is that a finite amount of different options can be processed more easily than a model with infinite possibilities. On the other hand restrictions are ruling out certain possibilities and do not fit to all models. When restrictions are applied to four dimensional models, they are acting like a filter that shows the essential information out of the unmanageable multitude. One application for this is the Lindenmayer-system. With it can be made path structures that remind of plants. Edited screencapture from Quantum Atomica Hypersphere structures are most evident on a size category of atoms. Location of electrons in the orbitals are calculated in probabilities. There are programs that calculate different kinds of electron-clouds. There the restrictions or filters are energy level of the electron, angular momentum and other options. Hyperspheres in Interaction This far there has been examined structure of a single hypersphere. Most interesting part of the four-dimensional properties is about interaction between the hyperspheres. Unlike the solid three-dimensional objects, hyperspheres not only can be overlapping with other hyperspheres, but they must be overlapping because of their infinite size. If a hypersphere is thought to be very fine mist, then can be thought that mist would be most dense where there is many hyperspheres close to each other. Hypersphere is an appearance of possibilities for all future positions. Certain dense area of the mist would refer that possibilities are more probable there. It is better to get back to example of coin toss. A coin can be fixed up to fall on other side more often. This will affect on a long term that the movement of the game piece is moving more to other of the two the directions. When hyperspheres are overlapping, they give an advantage of higher probability to move towards the direction of other hypersphere. If a force is affecting to the object, this causes increase of movement to the direction of the force. Once again it is necessary to go back to the coin toss example. The coin toss should be replaced with a roulette to produce uneven probabilities that are easily calculated. There are one hundred slots in the roulette, each of them representing a chance of one percentage. When force is applied to the object, it will give more than half of the probabilities to a specific direction. If chances of moving forwards would be two thirds of the slots, then the absolute movement in two directional space would be forwards two thirds of the time, and backwards one third of the time. This means that it is possible to calculate the relative movement by substracting the portition of moving backwards from portition of moving forwards. This speed of movement is one third of the total speed of absolute movement. This kind of calculation can be applied only for one dimensional movement, since there are more than two directions in higher dimensions. Next will be compared effects of equal force to objects that have different speeds of absolute movement. Force can be thought as a bonus for speed towards the specific direction. In this case force will give a bonus of speed for each movement forwards. There are two objects that have absolute movement speeds of one and two units. When the first object has the speed bonus that is one unit, it will double the difference of the absolute movements for going forwards and backwards. The other one has higher speed of the absolute movement, that is two units, and therefore a bonus of one unit is speeding up only two-thirds when compared to the opposite direction. This is also known as an inertia of the mass, as well as absolute movement is another, more geometrical description for mass. Connections between energy, mass and speed of light are clearly visible in world's most well known formula: "E=mc^2". 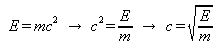Energy, mass and movement have the same nature, but the form of it varies. For each form there is most suitable purpose. Concept of movement fits best to examination of the gravitation. It is required to return to overlapping hyperspheres, since there is gravitational effect and nature visible. When hyperspheres are overlapping, their most dense part is the direct area between each other. Overlapping areas have ensemble effect. Where coin toss or roulette example was single-dimentional, with a two-dimensional example it would be more evident how objects affect to each other in the means gravitation. Two-dimensional example has an advantage to show what normally would happen in the fourth dimension, and at the same time it is familiar enough that it can be related to three-dimensional space. Forces of fourth dimension can be described with elevation and lower of a plane. A picture that describes a plane of this kind can be found from an earlier part of this article. If this plane would be replaced with some physical structure, then its attributes would remind of a water pool that has a very elastic rubber layer on it. That pool would have to be huge, a sea planet or an infinite plane. If it would be smaller than that, the tension of the surface would not be evenly divided. The same thing is noticeable when jumping in a trampoline. When you go closer to the edges, the higher tension will makes it harder to jump higher. Other option could be to calculate the surface tension and make the thickness of the rubber layer thinner from the edges to compensate the difference in the tension. In the next step two heavy balls are used to represent atoms and their effect. These balls are so heavy that they sink below the the surface, and at the same pull the rubber layer downwards. There are no other forces that would be affecting to the tension of the layer. Layer area between the balls has the highest tension, and therefore it is on a lower level than other areas. There is potential energy to roll into that direction, and so these balls start to move closer each other. 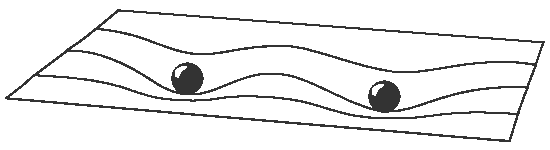There is a certain limit where boyancey of the water below will be stronger than the potential energy, which is produced by the effect of mass to layer's tension. This means that when these balls approach certain distance, they will find the shortest route around the middle point which is not possible for crossing. The balls will be driven to circle around the middle point. Epilogue and Recommendations Dear reader, if you have followed with interest elevation of a cube to higher dimension, I believe that you are eager to read more about infinities, concise dimensions and many other interesting subjects. I would like to recommend you, who are interested in dimensions, a few books that are telling about the subject in a popular way. "Hyperspace: A Scientific Odyssey Through Parallel Universes, Time Warps, and the 10th Dimension", written by Michio Kaku, is a book with a clear narration about dimensions of space and time. The history paragraph of this article is summary from those subjects in that book that I found essential for my own topic. There are also two illustrations from that book that I have lent. Although illustrations shown here have been available in the internet, they are still under copyrights of the author. I intend to ask a permission for use of those pictures with this article. Another book worth reading is "Infinity and the Mind - The Science and Philosophy of the Infinite", written by Rudy Rucker. The book in question is dealing with time, space and infinities mostly from a mathematical point of view. The third and most approachable publication is actually made in a form of a comic. "The Black Hole (The Adventures of Archibald Higgins)", written by Jean-Pierre Petit, is illustrating geometry of non-euclid pieces, and geometrical nature of physical phonomenon. If you might want to test the "Random Walk Generator". Testing out different options will make it easier to understand how the length of a step will affect to the dispersion. You also should try out "Quantum Atomica", if you are interested in probability clouds of hyperspheres or electron orbitals of atoms.